The theory of inflation is the leading paradigm for early-universe cosmology, playing a crucial role in generating cosmic perturbations that serve as the seeds for the formation of large-scale structures. The simplest inflationary scenarios are single-field models, among which are ultra slow-roll models which have gained attention from researchers as a mechanism for the formation of primordial black holes (PBHs). Primordial black holes are candidates for dark matter, which is essential for the structure formation in the universe. To form PBHs, the power spectrum on the relevant mass scales must grow by about seven orders of magnitude. The ultra slow-roll inflationary models provide the best mechanism for the rapid enhancement of the required power spectrum.
Recently, quantum loop corrections in ultra slow-roll models have been extensively studied, particularly in terms of whether these corrections could affect the perturbative behavior of the inflationary system and thus undermine the reliability of the PBH formation mechanism. In recent works, including this research, we have studied the effects of loop corrections on the power spectrum and the bispectrum of primordial perturbations. To compute the quantum corrections, it is necessary to derive the third- and fourth-order action and Hamiltonian for the perturbations. Performing these calculations using the conventional approach to quantum perturbations is highly complex and time-consuming. As a more efficient alternative, we employed effective field theory (EFT) methods and succeeded in deriving higher-order Hamiltonians, including the fourth-order Hamiltonian. We demonstrated that loop corrections can significantly influence the amplitude of non-Gaussianity and may violate observational constraints on the non-Gaussianity amplitudes. As a result, care must be taken when employing ultra-slow-roll inflationary models for the formation of primordial black holes.
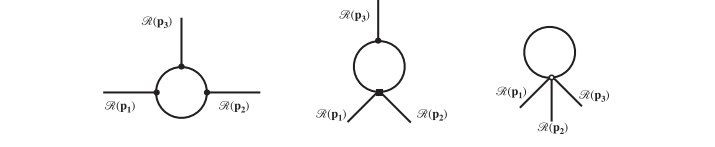
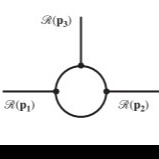
The one-particle irreducible Feynman diagrams for the one-loop corrections in bispectrum. In the left panel all three vertices come from H3 while in the middle panel the lower vertex is from H4 and the upper one is from H3. In the right panel there is a single vertex from H5.
